nLab convenient category of topological spaces
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Contents
Idea
The term convenient category of topological spaces is used (e.g. Steenrod 1967) for a category of topological spaces nice enough to address many of the needs of working topologists, notably including the condition of being a cartesian closed category. As such, they are examples of nice categories of spaces.
A primary example is the category of compactly generated spaces.
Definition
While the authors of this article don’t know whether there exists in the literature a widely accepted definition of “convenient category of topological spaces”, we propose the following definition as reasonable and convenient (see also the discussion below on the distinction between “nice” and “convenient”):
Definition
A convenient category of topological spaces is a full replete subcategory of the category of all topological spaces Top such that the following conditions 1-3 hold:
-
Every CW complex is an object of ;
-
is cartesian closed;
-
is complete and cocomplete.
Frequently it is also felt desirable to add closure under certain types of subspaces. For instance, in the well-known examples one has
- is closed under closed subspaces in Top, i.e., if belongs to and is a closed subspace (in ), then also belongs to .
At times one might hope that is closed under open subspaces as well, but this does not hold for all objects in some of the well-known examples of convenient categories.
It may be well to note that colimits and limits in need not agree with the corresponding colimits and limits in , except under certain conditions. Some convenient categories are reflective or coreflective in , in which case they are closed under limits or colimits respectively. Moreover, because is a full subcategory of which contains all CW complexes, the usual sorts of colimits used to present CW complexes are the same whether interpreted in or in . Also, if is closed under closed subspaces, then an equalizer of a pair of maps between Hausdorff spaces in (being a closed subspace) is the same whether computed in or in .
On the other hand, products of -objects in need not land in , so in that situation the product in and the product in do not agree. This is in particular the case for compactly generated spaces. In fact, the “compactly generated product” is sometimes preferable to the -product for more explicit reasons: for instance, if and are CW complexes, then need not be a CW complex in the usual product topology, but it is in the compactly generated topology.
Examples
Categories of colimits of generating spaces
The original example of a convenient category of topological spaces is that of
and another example is that of
Both of these are special cases of the general class of convenient -generated topological spaces:
These are those topological spaces which agree with the colimit (in TopSp) of all continuous images inside them of generating spaces in a specified full subcategory TopSp (Vogt 1971, Sec. 1):
The full subcategories of such -generated spaces are coreflective (Vogt 1971, Cor. 1.4)
If one demands of the category of generating spaces, for any pair that (Vogt 1971, Axiom 2):
-
their product topological space is again in ;
-
the compact-open topology on the set of maps has a continuous evaluation map
then is a Cartesian closed category (Vogt 1971, Thm. 3.6), with internal hom given by the image under -fication (1) of the compact open topology.
If one in addition demands that contains all topological simplices (or all Cartesian spaces ), then is a weak homotopy equivalence (Vogt 1971, Prop. 1.2 (g)).
As special cases of this general construction, the above examples of
-
compactly generated topological spaces is obtained by
taking to be given by all compact Hausdorff spaces
-
Delta-generated topological spaces is obtained by
taking to be given by all Cartesian spaces (equivalently by all topological simplices).
See also Gaucher 2007, Sec. 2.
Further developments along these lines are inEscardo, Lawson &Simpson 2004:
The topological spaces for which there is an exponentiable space in Top (i.e such that has a right adjoint) may be described more concretely as core-compact spaces (spaces whose topology is a continuous lattice). Suppose given a collection of core-compact spaces, with the property that the product of any two spaces in is a colimit in Top of spaces in . Such a collection is called productive. Spaces which are -colimits of spaces in are called -generated.
Theorem
(Escardó, Lawson, Simpson)
If is a productive class, then the full subcategory of whose objects are -generated is a coreflective subcategory of Top (hence complete and cocomplete) that is cartesian closed.
The other convenience conditions listed in this article (inclusion of CW-complexes, closure under closed subspaces) are in practice usually satisfied as well. For example, if closed subspaces of objects of are -generated, then closed subspaces of -generated spaces are also -generated. If the unit interval is -generated, then so are all CW-complexes.
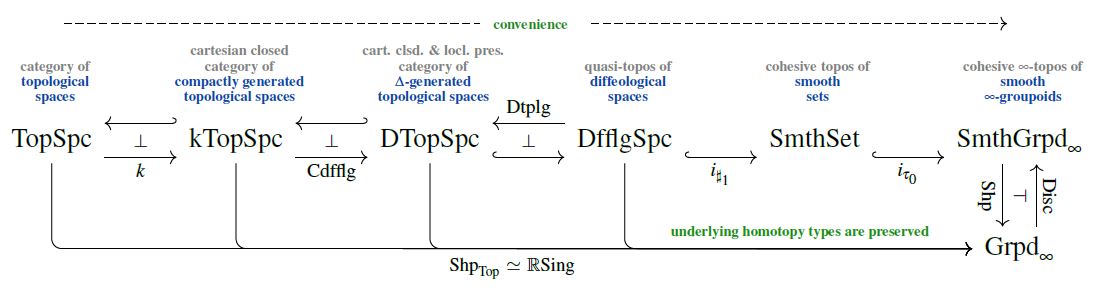
Subcategories of toposes
The above example of the category of Delta-generated topological spaces above has the remarkable property that it is
-
a full subcategory of the quasi-topos of diffeological spaces (see there),
-
which is in turn a full subcategory of the cohesive topos of smooth sets (see there);
-
which in turn is a full sub--category of the cohesive -topos of smooth -groupoids
such that the canonical shape modality (the smooth path ∞-groupoid construction) still sees the correct underlying homotopy type of topological spaces (SS20, Ex. 3.18, see also at model structure on Delta-generated topological spaces):
Counterexamples
A naive approach to the problem of constructing “convenient categories” usually runs into problems. For example, one could try to work with the full subcategory of consisting of exponentiable spaces; the problem is that even if and are exponentiable, the exponential may not be:
- The category of exponentiable spaces is not cartesian closed. (It is however cartesian: the product of two exponentiable spaces under the usual product topology is exponentiable.)
To see this, we recall that a Hausdorff space is exponentiable if and only if it is locally compact, and that an exponential (provided it exists) is Hausdorff if is. Thus, it is enough to exhibit two locally compact Hausdorff spaces , whose exponential is not locally compact.
Take with its usual topology and (the set of natural numbers) with the discrete topology. Suppose that an exponential exists in the category of locally compact Hausdorff spaces. Then it must be a countable product of copies of by the following calculation:
where the last functor in , in order to be representable, would have to be represented by a product . Using the universal property of products, one may easily exhibit a scalar multiplication
rendering a topological vector space (a TVS) over the real numbers. But it is well-known that locally compact TVS are finite-dimensional, and we have reached an absurdity.
Similarly, the topological product is homeomorphic to Baire space, and this is not locally compact either.
“Nice” versus “convenient” categories of spaces
A related entry is nice category of spaces. Here we explain the difference between “convenient” and “nice” categories of spaces.
“A convenient category of topological spaces” is the title of a well-known paper by Norman Steenrod, who emphasized particularly function space constructions (i.e., cartesian closure) as a great convenience for working algebraic topologists, on top of (generally less problematic) completeness and cocompleteness assumptions. (See also the historical remarks that follow.)
It is well-known that is not cartesian closed. One can characterize the exponentiable spaces, which include all locally compact Hausdorff spaces, but as we saw above, the naive idea of simply cutting down to some of these does not give a good cartesian closed category either, since firstly it need not be complete and cocomplete, and secondly even if and are exponentiable, the exponential need not be.
However, one can cut down to some full subcategory of spaces which does admit function spaces. This typically involves the subtle and delicate interplay between compactness conditions and openness conditions. It comes at a cost – that limits and/or colimits in the subcategory might not be computed as they are in – but this is generally considered a very small price to pay in exchange for the great convenience of these assumptions.
That a convenient category of topological spaces contains all the CW complexes was not explicitly declared by Steenrod, but we feel certain that algebraic topologists want these as part of their convenient category. In practice this is a mild assumption, because the usual examples certainly contain all finite topological products of the unit interval , and are closed under those -colimits used to present CW complexes, as built inductively from the basic spaces .
“Nice categories of spaces” should be thought of as a wider and vaguer term; it really means the category of spaces has “nice” categorical properties for some mathematical purpose at hand. Certainly any convenient category of spaces should be considered a nice category of spaces for the general purposes of algebraic topology. On the other hand, there are categories of spaces which are not “convenient” in the technical sense described above, but which may be very nice for certain purposes.
For example, the category of compact Hausdorff spaces can be considered as being very nice for certain purposes. For instance, it is monadic over (!) and a pretopos. It is, however, not “convenient”, as it is very far from being cartesian closed. In a different direction, there is the (complete, cocomplete) cartesian closed category of equilogical spaces, but this is not a full subcategory of , and the core concerns of mathematicians working with equilogical spaces are somewhat different from those of algebraic topologists.
It should also be noted that “space” itself has a wider meaning than the technical notion of “topological space”, even if topological intuitions come into play. For example, in domain theory, one often considers certain types of posets (for example, dcpos) as certain types of “spaces”. In this direction, we have that the category of dcpos and Scott-continuous maps between them forms a complete, cocomplete, cartesian closed category. However, these types of spaces are quite far removed from the traditional concerns of topology, hence are not “convenient” in the sense given above (despite the manifold relations between Scott continuity and the point-set topology which underlies the classical results on compactly generated spaces). In another direction, the category of locales is in some respects “nice”, but these are not topological spaces either.
Along with the entry on nice category of spaces and the examples above, see Johnstone's topological topos and Spanier’s quasitopological spaces (ref). None of these is convenient in the precise sense above. However there are advantages in having a category which is not only cartesian closed but also locally cartesian closed. In algebraic topology, this has led to Peter Booth’s work on “fibred mapping spaces” (ref), (ref).
There are possible advantages in homotopy theory of using a “topological topos”, (Johnstone ref), Harasani ref).
Historical remarks
The phrase “convenient category of topological spaces” predates Steenrod 1967 by a number of years; Brown 1963, Introduction says:
It may be that the category of Hausdorff -spaces is adequate and convenient for all purposes of topology.
The requirements for convenience were spelled out in Brown 1964.
In fact, Brown (not Steenrod, as has sometimes been assumed) was the first to prove that Hausdorff k-spaces (with the “kelleyfied” weakening of the compact–open topology on function spaces) formed what is now called a cartesian closed category (see Brown 1961), influenced by Cohen 1954.
Note Brown’s work predates the formal introduction of cartesian closed categories in Bill Lawvere‘s thesis by a couple of years; in fact there is clear anticipation in Brown’s thesis of the notions of monoidal closed and cartesian closed categories, which was to attract much attention throughout the sixties. Further, Brown’s results on the topological case are more precise than Steenrod’s, since the 1964 paper deals with functions continuous on compact subsets, and for these obtains a homeomorphism without kellyfication. An account of this may be found in the book Topology and Groupoids.
Of course, as has often been emphasized by Lawvere, the need for and convenience of considering function spaces is a very old idea in geometry (going back to the roots of the calculus of variations, for example). The constructions of exponentials of topological spaces via the compact–open topology had been known for a long time; see for example John Kelley‘s General Topology (1955). The relevance of what are today called Kelley spaces (or k-spaces1) had also been recognized; for example, Kelley’s book indicates the completeness of function spaces (wrt the compact–open topology) when the base is a complete uniform space and the exponent is a k-space. However, the problem of obtaining a class of spaces closed under function spaces wasn’t solved prior to Brown’s thesis. Brown also observed the relevance of k-spaces to studies of how products interact with quotient spaces. The general appreciation of the connection between cartesian closure and preservation of quotients under products came with the appreciation of the conceptual simplicity of categorical adjunctions, namely the point that the functor preserves colimits if it has an exponential right adjoint . The question also solved in Brown’s 1964 paper was to give, in the Hausdorff case, a left adjoint to the functor when the function spaces have the compact-open topology, and so to give a monoidal closed structure on the category of Hausdorff spaces; the generalisation to the non-Hausdorff case is given in the paper of Booth and Tillotson listed below.
Appreciation of the role of convenient categories was in full force by the early seventies (for a sample, see Peter May‘s Geometry of Iterated Loop Spaces, where the category of Hausdorff k-spaces plays a foundational role). The notion of a “convenient category” is recognized elsewhere too (and not just within the categorical and algebraic topology communities); see for example the book by Kriegl and Michor.
Related concepts
References
The terminology (“convenient category of topological spaces”) became widely adopted with
- Norman Steenrod, A convenient category of topological spaces, Michigan Math. J. 14 (1967) 133–152 (euclid:mmj/1028999711)
referring there to the category of compactly generated topological space (see the references there for more), whose convenient cartesian closure had previously been highlighted in:
-
Ronnie Brown, Some problems of algebraic topology: a study of function spaces, function complexes, and FD-complexes, DPhil thesis, Oxford University, 1961 (Note: the Appendix of this thesis was withdrawn from the examination.) (pdf)
-
Ronnie Brown, Ten topologies for , Quart. J.Math. (2) 14 (1963), 303–319. (doi:10.1093/qmath/14.1.303, pdf)
-
Ronnie Brown, Function spaces and product topologies, Quart. J. Math. (2) 15 (1964), 238–250. (doi:10.1093/qmath/15.1.238)
influenced, in turn, by:
- D. E. Cohen, Spaces with weak topology, Quart. J. Math., (2) 5 (1954) 77–-80 (doi:10.1093/qmath/5.1.77)
Discussion in the generality that subsumes compactly generated topological spaces and Delta-generated topological spaces and all cases of subcategory-generated spaces in between:
-
Rainer M. Vogt, Convenient categories of topological spaces for homotopy theory, Arch. Math 22, 545–555 (1971) (doi:10.1007/BF01222616)
-
Oswald Wyler, Convenient categories for topology, General Topology and its Applications 3 3 (1973) 225-242 (doi:10.1016/0016-660X(72)90014-1)
-
Martín Escardó, Jimmie Lawson, Alex Simpson, Section 3 of: Comparing Cartesian closed categories of (core) compactly generated spaces, Topology and its Applications Volume 143, Issues 1–3, 28 August 2004, Pages 105-145 (doi:10.1016/j.topol.2004.02.011)
-
Lisbeth Fajstrup, Jiří Rosický, Section 3 of: A convenient category for directed homotopy, Theory and Applications of Categories, Vol. 21, 2008, No. 1, pp 7-20. (arXiv:0708.3937, tac:21-01)
-
Philippe Gaucher, Section 2 of: Homotopical interpretation of globular complex by multipointed d-space, Theory and Applications of Categories, vol. 22, number 22, 588-621, 2009 (arXiv:0710.3553)
On the abstract construction principle of these examples:
- Michael Barr, Building closed categories, Cahiers Topologie Géométrie Différentielle 19 (1978) 115–129 [numdam:CTGDC_1978__19_2_115_0]
See also:
-
Edwin Spanier, Quasi-topologies, Duke Mathematical Journal 30 (1) (1963), 1–14.
-
Peter I. Booth, The exponential law of maps. II. Math. Z. 121 (1971), 311–319.
-
P. Booth, ; Tillotson, J., Monoidal closed, Cartesian closed and convenient categories of topological spaces. Pacific J. Math. 88 (1980), no. 1, 35–53. project euclid
-
Michael Crabb, Ioan James , Fibrewise homotopy theory. Springer Monographs in Mathematics. Springer-Verlag London, Ltd., London, 1998. viii+341 pp. ISBN: 1-85233-014-7
-
Gerhard Preuß, Foundations of topology: an approach to convenient topology, Kluwer, Dordrecht/ Boston 2002 (doi:10.1007/978-94-010-0489-3)
survey in: Convenient topology – a new branch of topology (web)
-
Ronnie BrownTopology and Groupoids, Booksurge (2006), available from amazon: Section 5.9: Spaces of functions and the compact-open topology.
Discussion via topos theory:
-
Peter Johnstone, On a topological topos, Proc. London Math. Soc. (3) 38 (1979) 237–271.
-
Harasani, Hamed A. Topos theoretic methods in general topology, PhD Thesis, University of Wales, Bangor, (1988) (link to pdf files).
Analogous considerations for diffeological spaces (subsuming D-topological spaces)
- Andreas Kriegl; Peter Michor, The Convenient Setting of Global Analysis, Mathematical Surveys and Monographs, Volume 53. American Mathematical Society, Providence, RI (1997).
-
The ‘’ certainly refers to ‘kompakt’ rather than Kelley’s initial. ↩
Last revised on November 4, 2023 at 07:13:54. See the history of this page for a list of all contributions to it.